Matematica: limbajul Universului

Hai să discutăm azi despre Univers. S-ar putea ca acest articol să nu fie ceea ce vă așteptați.

Atunci când ne propunem să vorbim despre întregul Univers trebuie să ne imaginăm o poveste plină de evenimente minunate, cum ar fi colapsul stelelor, coliziunile galactice, proprietăţile ciudate ale particulelor și chiar degajările catastrofale de energie.

V-ați putea aștepta la o poveste ce s-ar întinde în timp de la evenimentul Big Bang și până în prezent. Desigur, această poveste este importantă. Dar mai există aici un aspect al acestor evenimente uimitoare care este adeseori trecut cu vederea, cel puţin până când încercaţi cu adevărat să înţelegeţi ce se întâmplă cu adevărat.

În spatele tuturor realizărilor noastre de până acum există un instrument care ne permite să descoperim lucrurile despre care ne place să învăţăm. Acest instrument este matematica, iar fără ea Universul ar fi încă învăluit în întuneric.

În acest articol voi încerca să vă conving că matematica nu este o ştiinţă arbitrară, inutilă, ci vă voi arăta că ea este un limbaj pe care îl folosim pentru a comunica cu stelele.

În prezent suntem legaţi de sistemul nostru solar. Această afirmaţie este de fapt mai bună decât pare, deoarece a fi legați de sistemul nostru solar este un pas important înainte în comparaţie cu situaţia de a fi legați, pur și simplu, de planeta noastră, așa cum am fost înainte ca unele genii ale omenirii să-şi îndrepte atenția spre cer.

Înainte de Galileo, cel care a utilizat telescopul pentru a studia cerul, sau Kepler, cel care a descoperit că traiectoria planetelor în jurul Soarelui este o elipsă, sau Newton, cel care a descoperit constanta gravitațională, matematica pe care o cunoșteam era oarecum limitată, iar înțelegerea noastră asupra Universului era destul de ignorantă.

În esența sa, matematica permite unei specii care este legată de sistemul său solar să sondeze adâncurile Cosmosului din fața unui birou. Pentru a aprecia cât de importantă este matematica, trebuie mai întâi să facem un pas înapoi și să privim către începuturile sale și la modul prin care aceasta este atât de strâns legată de existența noastră.

Un moment definitoriu pentru omenire. Galileo Galilei își îndreaptă telescopul spre cer.

Mai mult ca sigur, matematica a apărut în cadrul triburilor umane foarte timpurii (anterior culturii babiloniene căreia îi sunt atribuite unele dintre primele calcule matematice din istorie) care au utilizat matematica ca pe o modalitate de a ține evidența ciclurilor lunare sau solare și pentru înregistrarea numărului de animale, alimente, etc.

Este la fel de natural ca atunci când copii fiind am putut vedea că o jucărie în plus faţă de o altă jucărie însemna că avem mai mult de o jucărie. Pe măsură ce am crescut, am înţeles că 1 + 1 = 2 și că această aritmetică simplă pare a fi întrețesută în însăşi natura noastră.

Cei care pretind că nu au abilităţi matematice greşesc, deoarece aşa cum toți putem respira sau clipi din ochi, cu toții avem această capacitate înnăscută de a înțelege aritmetica.

Matematica este atât o prezență naturală, cât şi o ştiinţă umană. Se pare că natura ne oferă această capacitate de a recunoaşte modele într-o formă aritmetică, iar noi am construit sistematic mai multe sisteme matematice complexe care nu sunt evidente în natură, dar care ne permit să comunicăm în continuare cu natura.

O tăbliță din cultura babiloniană pe care se pot observa simboluri matematice.

Matematica s-a dezvoltat odată cu evoluţia umană într-un mod similar în cadrul fiecărei culturi umane. Este uimitor să constatăm că deşi unele culturi umane nu s-au aflat în contact unele cu altele, matematica s-a dezvoltat în interiorul acestora într-un mod similar. Cu toate acestea, doar atunci când omenirea a utilizat matematica pentru a studia cerul putem spune că aceasta a început cu adevărat să se dezvolte într-un mod uimitor.

Nu este o simplă coincidență faptul că revoluția științifică a fost impulsionată de dezvoltarea matematicii, care a fost aplicată pentru a ajuta la înțelegerea locului nostru în Univers. Din momentul în care Galileo a măsurat viteza cu care cad obiectele, într-o încercare de a arăta matematic că masa unui obiect nu influențează această viteză, viitorul omenirii s-a schimbat pentru totdeauna.

Acesta este momentul în care perspectiva noastră cosmică asupra Universului s-a schimbat cu ajutorul matematicii. Fără aceasta am fi putut crede în continuare că ne aflăm pe una dintre planetele care orbitează în jurul unei stele aflată în mijlocul unui fundal luminos aparent nemișcat.

Aceasta este o perspectivă destul de sumbră în comparație cu ceea ce ştim acum despre Universul în care trăim. Această idee asupra Universului ne motivează să înțelegem mai multe despre matematica utilizată de Johannes Kepler atunci când a observat mscarea planetelor, această matematică aplicată permiţându-i acestuia să dezvolte un model destul de precis a Sistemului Solar și o metodă pentru estimarea mișcării planetelor. Aceasta este una dintre numeroasele demonstrații care ilustrează importanța matematicii în istoria noastră, în special în cadrul astronomiei şi fizicii.

Johannes Kepler a folosit matematica pentru a-și modela observațiile cu privire la mișcarea planetelor.

Povestea matematicii devine și mai uimitoare odată cu unul dintre cei mai importanţi oameni de ştiinţă ai umanităţii. Atunci când Sir Isaac Newton a studiat mişcarea cometei Halley, a înțeles că matematica care a fost utilizată până atunci pentru a descrie mișcarea obiectelor masive, pur și simplu nu este suficientă pentru a înțelege vreodată ceva ce se află dincolo de orizontul nostru limitat.

Printr-o genială intuiție, care confirmă afirmația mea de mai înainte despre cum putem folosi ceea ce avem în mod natural pentru a construi ulterior un sistem mai complex, Newton a dezvoltat o metodă de calcul prin care a fost capabil să descrie cu exactitate mișcarea nu doar a cometei Halley, dar, de asemenea, a oricărui alt corp care se deplasează pe bolta cerească.

Isaac Newton

Într-o singură clipă întregul Univers s-a deschis în fața noastră, oferindu-ne posibilităţi aproape nelimitate de a conversa cu acesta.

Newton a dezvoltat în continuare lucrările începute de Kepler. El și-a dat seama că ecuația matematică a lui Kepler pentru mișcarea planetelor, a treia lege a lui Kepler (p^2 = A^3), s-a bazat exclusiv pe observația empirică și că aceasta a fost menită doar pentru a descrie ceea ce s-a observat în Sistemul Solar.

Newton a înţeles că această ecuație de bază ar putea fi generalizată prin aplicarea unei constante gravitaționale, ceea ce a dat naștere la, probabil, una dintre cele mai importante ecuații care a fost obţinută vreodată de omenire: versiunea lui Newton pentru cea de-a treia lege a lui Kepler.

Se poate vedea că cea de-a treia lege a lui Kepler rămâne valabilă şi că prin adăugarea valorilor pentru constanta gravitațională G și pentru masele M și m ale celor două corpuri în cauză această ecuație nu mai este limitată doar la sistemul nostru solar.

Newton a înţeles că atunci când corpurile se mişcă într-un mod neliniar, dacă vom folosi algebra de bază nu vom obţine o descriere corectă a mişcării.

Algebra ne permite să găsim panta (rata schimbării) în cazul unor linii drepte (rată constantă de schimbare), în timp ce calculul diferenţial ne permite să găsim panta liniilor curbe (rată variabilă de schimbare). Evident, există mai multe aplicații ale calculului diferențial în afară de ce am arătat aici, dar eu am vrut doar să ilustrez o diferență fundamentală între cele două metode de calcul în scopul de a vă arăta cât de revoluționar a fost acest nou concept.

Dintr-o dată, mișcările planetelor și a altor obiecte care orbitează Soarele au putut fi determinate mai precis și astfel s-a putut înțelege puțin mai profund Universul.

Revenind la versiunea lui Netwon pentru cea de-a treia lege a lui Kepler, am avut astfel posibilitatea de a aplica (și încă o facem) această ecuație incredibilă în cazul oricărui obiect aflat în mişcare de rotaţie în jurul altui obiect. Din această ecuație putem determina masa obiectelor, distanța dintre acestea, forța de gravitație care se exercită între cele două corpuri și alte mărimi fizice.

Newton a fost astfel capabil să obțină valoarea constantei gravitaționale pentru toate obiectele din Univers (G = 6,672 × 10^-11 Nm^2 kg^-2). Această constantă i-a permis să unifice astronomia şi fizica şi să poată prezice mişcarea corpurilor în Univers. S-au putut determina masele planetelor (și a Soarelui) cu o mai mare precizie, aplicând pur și simplu fizica newtoniană (numită astfel pentru a onora importanţa lui Newton din fizică și matematică).

Noi am putut aplica Cosmosului acest nou limbaj pentru a încerca să-i înţelegem secretele. Acesta a fost un alt moment definitoriu pentru omenire, un moment în care toate acele lucruri care înainte nu putea fi cunoscute au devenit accesibile înţelegerii noastre prin utilizarea noilor metode matematice. În acest fel am putut înţelege limbajul stelelor.

Probabil cea mai bună ilustrare a puterii pe care matematica ne-a dat-o este descoperirea planetei Neptun. Până la descoperirea acesteia în septembrie 1846, planetele au fost descoperite doar prin observarea unor „stele” care se mişcau într-un mod ciudat în raport cu stelele de pe bolta cerească. Numele de planetă provine din cuvântul din limba greacă pentru „rătăcitor”, astfel fiind descrise aceste „stele” a căror mişcare pe bolta cerească descria anumite tipare specifice vizibile în diferite perioade ale anului.

Atunci când Galileo a îndreptat pentru prima oară telescopul său spre cer, aceste obiecte pribege s-au dovedit a fi alte lumi care păreau a fi similare cu planeta noastră. De fapt unele dintre aceste lumi păreau a fi sisteme solare de mici dimensiuni, aşa cum Galileo a descoperit atunci când a început observarea sateliţilor lui Jupiter.

După ce Newton şi-a prezentat ecuațiile sale, matematicienii au fost încântați să le aplice în studiul mişcării corpurilor cereşti. S-a început cu determinarea mișcărilor planetelor și s-au obţinut modele mai exacte pentru traiectoriile acestora.

S-au folosit aceste ecuații pentru a aproxima masa Soarelui. S-au putut face previziuni remarcabile care au fost validate în timp prin noi observaţii. Era ceva fără precedent, folosind matematica se puteau face predicții la care nimeni nu s-ar fi gândit niciodată, iar apoi folosind observaţiile reale se putea verifica corectitudinea calculelor matematice.

Cu toate acestea, s-au observat unele discrepanțe ciudate în legătură cu anumite lucruri. Uranus, de exemplu, nu se mişca aşa cum ar trebui, conform legilor lui Newton.

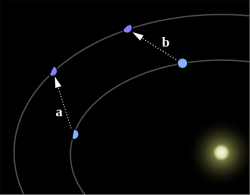Se poate vedea că planeta interioară este perturbată de planeta exterioară. În cazul nostru planeta exterioară a fost Neptun, cea care a fost descoperită în acest fel.

Descoperirea lui Neptun a fost deosebită tocmai prin modul în care a avut loc. Newton a fost cel ce a descoperit un limbaj mai profund al Cosmosului, prin care Universul ni s-a dezvăluit mai mult. Și exact acest lucru s-a întâmplat atunci când am aplicat acest limbaj în cazul orbitei lui Uranus.

Neptun este mai mult decât a opta planeta din Sistemul Solar. Ea este un memento ceresc privind puterea pe care matematica ne-a acordat-o.

Modul ciudat în care Uranus orbita în jurul Soarelui nu se potrivea cu ceea ce ar fi trebuit să observăm, dacă aceasta era singura planetă aflată la acea distanță de Soare. Privind la numere, trebuia să mai fie altceva acolo care-i perturba orbita.

Înainte de intuiția și legile matematice ale lui Newton n-am fi avut niciun motiv să suspectăm că ceva era greşit în ceea ce observam. Uranus orbita în jurul Soarelui, aşa cum a făcut-o şi în trecut. Prin recunoaşterea faptului că matematica este un dialog cu Universul, odată ce am formulat întrebarea în mod corect ne-am dat seama că există într-adevăr ceva dincolo de ceea ce puteam vedea în mod direct. Aceasta este frumuseţea matematicii, o conversație cu Universul prin care putem cunoaște mai multe decât ne așteptăm.

Matematicianul francez Urbain Le Verrier a fost cel care a lucrat cu migală la ecuaţiile matematice ale orbitei lui Uranus. Folosind ecuațiile matematice ale lui Newton, acesta a înţeles că trebuie să existe un alt obiect cosmic aflat dincolo de orbita lui Uranus şi care, de asemenea, orbitează în jurul Soarelui.

Verrier a încercat să determine ce masă ar trebui să aibă acel corp ceresc şi la ce distanţă trebuie să se afle faţă de Soare pentru a perturba orbita lui Uranus aşa cum s-a observat. Acest lucru a fost fenomenal, din moment ce s-a identificat o planetă pe care nimeni nu a observat-o vreodată, utilizând doar pergament şi cerneală.

Verrier a înţeles că trebuie să existe o planetă, denumită Neptun, care orbitează la o anumită distanță de Soare şi care are o anumită masă ce perturbă orbita lui Uranus. Încrezător în calculele sale matematice el s-a deplasat la New Berlin Observatory acolo unde astronomul Johann Gottfried Galle a privit către locul de pe bolta cerească indicat de calculele lui Verrier și a reuşit să observe cea de-a opta planetă a sistemului nostru solar, aflată la mai puțin de 1 grad diferenţă faţă de poziţia rezultată din calculele lui Verrier. Aceasta a fost o confirmare incredibilă a teoriei gravitaționale a lui Newton și a dovedit că matematica utilizată de acesta a fost corectă.

Urbain Le Verrier

Aceste descoperiri matematice au continuat mult timp după Newton. Am putut învăţa mai multe despre Univers odată cu noile progrese din matematică.

În secolul 20 teoria cuantică a început să prindă contur și în curând oamenii au înțeles că fizica newtoniană și matematica sa par să nu aibă nicio putere asupra a ceea ce s-a observat la nivel cuantic.

Un nou progres important în matematică a avut loc odată cu Albert Einstein. Acesta a prezentat teoria relativităţii restrânse şi teoria generală a relativităţii care au stabilit un nou mod de a înţelege nu numai gravitația, dar, de asemenea, energia și Universul în general. Matematica lui Einstein ne-a permis să descoperim un dialog mai profund cu Universul prin care am început să înțelegem originile sale.

Ecuația lui Einstein pentru echivalența dintre masă şi energie a reprezentat un alt progres incredibil pentru omenire. Credit: Pixabay.

În prezent am înţeles că există două ramuri ale fizicii care nu se potrivesc în totalitate. Fizica newtoniană sau fizica „clasică” care se poate aplica extraordinar de bine la o scară dimensională foarte mare (mișcarea planetelor, galaxiilor, etc…) şi fizica cuantică, cea care se poate aplica la o scară dimensională foarte mică şi care explică interacțiunile particulelor subatomice, lumina, etc…

Aceste două domenii ale fizicii sunt ireconciliabile, la fel ca două dialecte diferite ale unei limbi. Ele sunt similare și ambele funcţionează, dar nu se potrivesc între ele. Una dintre cele mai mari provocări cu care ne confruntăm în prezent este reprezentată de încercarea de realizare a unei „teorii a totului” care să unească legile din lumea cuantică cu legile din lumea macroscopică. Aceasta ar urma să explice tot ce există în Univers doar în termenii mecanicii cuantice. Nu este o sarcină ușoară, dar se încearcă rezolvarea acestei probleme.

După cum puteți vedea, matematica este mai mult decât un set de ecuații vagi și reguli complexe pe care trebuie să le memoraţi. Matematica este limbajul Universului și în procesul de învățare acest limbaj ne permite să înţelegem mecanismele de bază prin care funcţionează Cosmosul.

Este la fel ca atunci când călătoriţi într-o ţară străină și treptat începeţi să înţelegeţi limba vorbită acolo. Acest demers matematic este cel ce ne permite să explorăm adâncurile Universului. Fiind o specie legată de sistemul nostru solar nu avem nicio posibilitate să călătorim până în centrul galaxiei noastre pentru a confirma vizual că există acolo o gaură neagră supermasivă.

Nu avem posibilitatea să ne aventurăm într-o nebuloasă stelară pentru a urmări în timp real naşterea unei stele. Cu toate acestea, cu ajutorul matematicii, putem să înțelegem toate aceste caracteristici ale Universului. Atunci când învăţaţi matematica, nu doar vă îmbogăţiţi cunoștințele, dar vă şi conectați cu Universul la un nivel fundamental.

De la birou puteţi explora orizontul evenimentului unei găuri negre sau mărturia furiei distructive din spatele unei explozii de supernovă. Toate acele lucruri pe care le-am menționat pot fi studiate cu ajutorul matematicii. Marea poveste a Universului este scrisă în limbajul matematicii și capacitatea noastră de a traduce aceste valori numerice în evenimente despre care tuturor ne place să învăţăm este uimitoare.

În concluzie, amintiţi-vă atunci când învăţaţi matematica că aceasta ne conectează la stele.

Suntem conectaţi cu Universul prin intermediul matematicii.

Traducere şi adaptare după Mathematics: The Beautiful Language of the Universe