Frumuseţea matematicii: cele mai frumoase ecuații în imagini

Mulți oameni de știință recunosc adeseori că sunt pasionați de formulele matematice şi nu doar pentru utilitatea lor, ci şi pentru forma și informaţiile pe care le dezvăluie.

Frumusețea matematicii. Credit: Shutterstock/Fedorov Oleksiy

În timp ce anumite ecuații celebre, cum ar fi E = mc^2 a lui Albert Einstein, au devenit populare în rândul pasionaţilor de ştiinţă, altele sunt cunoscute mai mult oamenilor de știință.

LiveScience a încercat să afle ecuaţiile preferate ale unor fizicieni, astronomi și matematicieni, iar răspunsurile găsite sunt rezumate în cele ce urmează.

Relativitatea generală

Ecuația din imaginea de mai jos a fost formulată de Einstein în anul 1915 ca parte a teoriei relativităţii generale. Această teorie a revoluționat modul în care oamenii de știință au înțeles gravitația, o deformare a spațiu-timpului.

Relativitatea generală. Credit: Shutterstock/RT Wohlstadter

„Este încă uimitor pentru mine că o astfel de ecuație matematică poate descrie ce este spațiu-timpul. Tot geniul lui Einstein este exemplificat prin această ecuație”, a declarat astrofizicianul Mario Livio din cadrul Space Telescope Science Institute, care a indicat această ecuație drept favorita lui.

„Partea din dreapta a acestei ecuații descrie conținutul de energie al Universului, inclusiv energia întunecată care provoacă expansiunea accelerată a Universului. Partea din stânga descrie geometria spațiu-timpului.

Egalitatea reflectă faptul că, în relativitatea generală a lui Einstein, masa și energia determină geometria și concomitent curbura spaţiu-timpului, care este o manifestare a ceea ce numim gravitație”, a explicat Livio.

„Această ecuație foarte elegantă relevă relația dintre spațiu-timp, materie și energie şi explică modul prin care Soarele deformează spațiu-timpul astfel încât Pământul şi celelalte planete ale Sistemului Solar se mișcă în jurul lui pe diferite orbite.

De asemenea, această ecuaţie poate fi utilizată pentru a descrie evoluţia Universului de la momentul Big Bang și prezice existenţa găurilor negre„, a declarat Kyle Cranmer, fizician în cadrul New York University.

Modelul Standard

Modelul Standard este o altă teorie de bază din fizica actuală care descrie particulele elementare despre care fizicienii cred că formează Universul.

Modelul Standard. Credit: Shutterstock/RT Wohlstadter

Ecuaţia Modelului Standard din imaginea de mai sus poate fi integrată într-o ecuație principală denumită modelul standard „lagrangian” (după numele lui Joseph Louis Lagrange, un matematician și astronom francez din secolul al XVIII-lea). Aceasta este ecuaţia preferată de fizicianul teoretician Lance Dixon din cadrul SLAC National Accelerator Laboratory.

„Modelul Standard a descris cu succes toate particulele elementare și forțele pe care le-am observat în laborator până în prezent, cu excepția gravitației. El include, desigur, bosonul Higgs recent descoperit.

Modelul Standard este perfect compatibil cu mecanica cuantică și relativitatea specială”, a declarat Dixon pentru LiveScience.

Teoria Modelului Standard nu a fost încă unificată cu relativitatea generală, motiv pentru care ea nu descrie gravitația.

Integrala

În timp ce primele două ecuații descriu aspecte particulare ale Universului, o altă ecuație preferată de oamenii de ştiinţa poate fi utilizată într-o mulţime de situaţii practice.

Teorema fundamentală a calculului integral indică relaţia dintre cele două operaţii principale ale sale, derivarea şi integrarea.

Integrala. Credit: Shutterstock/agsandrew

„În cuvinte simple, integrala arată că variaţia netă a unei mărimi continue, precum ar fi distanța parcursă într-un interval de timp dat (adică diferența valorilor acelei mărimi în punctele finale ale intervalului de timp) este egală cu integrala vitezei de variaţie a acelei mărimi, adică integrala vitezei”, a declarat Melkana Brakalova-Trevithick, președintele departamentului de matematică al Fordham University.

Pentru Trevithick, integrala este ecuația ei favorită.

„Teorema fundamentală a calculului integral ne permite să determinăm variaţia netă pe un interval pe baza ratei schimbării pe întregul interval”, a declarat Trevithick.

Bazele calculului integral provin din cele mai vechi timpuri, dar o mare parte din acestea au fost stabilite în secolul al XVII-lea de Isaac Newton, care a utilizat calculul integral pentru a descrie mişcările planetelor în jurul Soarelui.

Teorema lui Pitagora

Teorema lui Pitagora este învăţată de fiecare elev la cursul de geometrie.

Formula lui Pitagora arată că în orice triunghi dreptunghic pătratul lungimii ipotenuzei (cea mai lungă latură a unui triunghi dreptunghic) este egal cu suma pătratelor lungimilor celorlalte două laturi.

Teorema lui Pitagora. Credit: Shutterstock/igor. Stevanovic

„Prima formulă matematică care m-a uimit a fost cea a lui Pitagora. Pe atunci eram un copil și mi s-a părut atât de uimitor că aceasta se aplică în geometrie și funcționează cu numere!”, a declarat matematicianul Daina Taimina de la Cornell University.

Ecuația lui Euler

Această formulă simplă descrie o proprietate importantă a sferelor:

„Dacă tăiați suprafața unei sfere în fețe, muchii și vârfuri, astfel încât F este numărul de fețe, E este numărul de muchii și V este numărul de vârfuri, veți obține întotdeauna V-E+F=2″, a declarat Colin Adams, matematician din cadrul Williams College din Massachusetts.

Ecuația lui Euler. Credit: Shutterstock/Jezper

„Ca exemplu, un tetraedru este format din 4 triunghiuri, 6 laturi sau muchii și 4 vârfuri. Dacă am sufla puternic într-un tetraedru cu fețe flexibile, putem să-l rotunjim într-o sferă, astfel încât, în acest sens, o sferă poate fi tăiată în 4 fețe, 6 muchii și 4 vârfuri.

Observăm astfel că pentru tetraedru V-E+F=2, iar același lucru este valabil pentru o piramidă cu 5 fețe, 4 triunghiuri și un pătrat, 8 laturi și 5 vârfuri și pentru orice altă combinație de fețe, muchii și vârfuri.

Această relaţie dintre numărul vârfurilor, muchiilor și fețelor descrie un aspect fundamental în ceea ce privește forma unei sfere”, a explicat Adams.

Relativitatea specială

Einstein se regăseşte din nou în această listă cu formulele sale pentru relativitatea specială, care arată că timpul și spațiul nu sunt concepte absolute, ci mai degrabă sunt relative în funcție de viteza observatorului.

Ecuația din imaginea de mai jos arată dilatarea timpul, din relativitatea specială, în funcţie de viteza de deplasare.

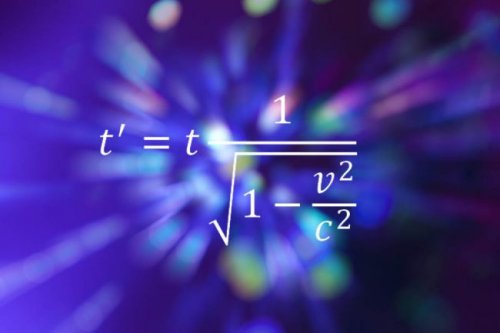
Relativitatea specială. Credit: Shutterstock/Optimarc

„Această ecuaţie foarte simplă, fără derivate complexe, reprezintă un mod cu totul nou de a înţelege lumea și relația noastră cu aceasta. Deodată, cosmosul rigid şi neschimbat este înlocuit cu o lume personală, legată de tot ceea ce observăm”, a declarat Bill Murray, fizician în cadrul CERN din Geneva.

Murray preferă ecuațiile din relativitatea specială față de formulele mai complicate din teoria reltivitatii generale. „Nu am putut niciodată să urmăresc matematica relativității generale”, a declarat Murray.

1 = 0,999999999…

Această ecuație simplă, care afirmă că valoarea 0,999 urmată de un șir infinit de 9, este echivalentă cu 1, este preferata matematicianului Steven Strogatz de la Cornell University.

Credit: Shutterstock/Tursunbaev Ruslan

„Îmi place cât de simplă este această ecuaţie. Toată lumea înțelege semnificaţia ei şi totuși este atât de provocatoare.

Partea stângă a ecuaţiei reprezintă începutul matematicii, iar partea dreaptă reprezintă misterul infinitului”, a declarat Strogatz.

Ecuațiile Euler-Lagrange și teorema lui Noether

„Aceste ecuaţii sunt destul de abstracte, dar uimitor de puternice. Cel mai important este că acest mod de a gândi despre fizică a rezistat unor revoluții majore în fizică, precum mecanica cuantică, relativitatea, etc”, a declarat Cranmer din cadrul New York University.

Ecuațiile Euler-Lagrange. Credit: Shutterstock/Marc Pinter

L din formulă reprezintă „lagrangianul”, care este o măsură a energiei într-un sistem fizic, cum ar fi arcuri, pârghii sau particule fundamentale. „Prin rezolvarea acestei ecuații aflăm cum va evolua un sistem în timp”, a declarat Cranmer.

Teoremă lui Noether a fost denumită după numele lui Emmy Noether, un matematician german din secolul XX.

„Această teoremă este într-adevăr fundamentală pentru fizică și rolul simetriei. Dacă un sistem are o simetrie, atunci există o lege de conservare corespunzătoare. De exemplu, ideea că legile fundamentale ale fizicii sunt aceleași astăzi şi mâine (simetria timpului) implică faptul că energia se conservă.

Ideea că legile fizicii sunt aceleași aici, dar şi în altă parte, implică faptul că impulsul se conservă. Simetria este un concept de bază în fizica fundamentală datorită contribuției lui Noether”, a declarat Cranmer.

Ecuația Callan-Symanzik

Ecuația Callan-Symanzik are numeroase aplicații, inclusiv estimarea masei și mărimii protonului și neutronului, care alcătuiesc nucleul atomilor.

Ecuația Callan-Symanzik. Credit: Shutterstock/RT Wohlstadter

Fizica ne spune că forța gravitațională și forța electrică dintre două corpuri sunt proporționale cu inversul distanței dintre cele două corpuri la pătrat.

Același lucru este valabil și pentru forța nucleară tare care leagă protonii și neutronii împreună pentru a forma nucleele atomilor și care, de asemenea, leagă quarcurile ce formează protonii și neutronii. Cu toate acestea, fluctuațiile cuantice minuscule pot modifica ușor dependența acestei forțe în funcţie de distanță, ceea ce are consecințe dramatice asupra intensităţii forței nucleare tari.

„Acest efect împiedică diminuarea acestei forțe la distanțe mari și astfel quarcurile se pot uni pentru a forma protonii și neutronii. Ecuația Callan-Symanzik asociază acest efect important și dificil de calculat, atunci când distanța este aproximativ egală cu dimensiunea unui proton, cu efecte mai subtile, dar mai ușor de calculat, care pot fi măsurate atunci când distanța este mult mai mică decât cea a unui proton”, a declarat fizicianul teoretician Matt Strassler de la Rutgers University.

Ecuația suprafeţei minime

„Ecuația suprafeţei minime codifică cumva peliculele frumoase de săpun care se formează atunci când scufundăm un fir de sârmă într-o apă cu săpun.

Faptul că această ecuație este „neliniară”, implică puteri și produse de derivate, este un indiciu matematic codificat privind comportamentul surprinzător al peliculelor de săpun.

Ecuația suprafeţei minime. Credit de imagine: Hubble

Această caracteristică contrastează cu ecuațiile diferențiale parţiale liniare mai familiare, precum ecuația căldurii, ecuația undelor și ecuația Schrödinger din mecanica cuantică”, a declarat matematicianul Frank Morgan de la Williams College.

Linia Euler

Glen Whitney, fondatorul Muzeului de Matematică din New York, a ales o altă teoremă geometrică, aceasta având de-a face cu linia Euler, denumită după Leonhard Euler, un matematician și fizician elvețian din secolul al XVIII-lea.

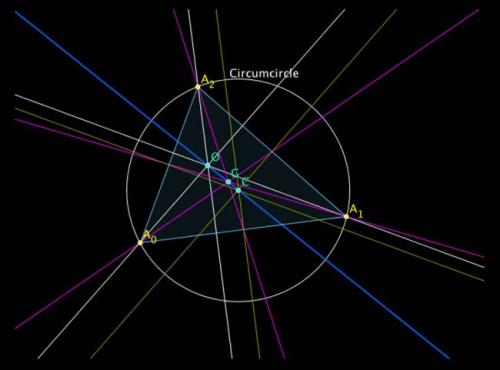
Linia Euler. Credit: Patrick Ion

„Desenati orice triunghi si găsiţi cercul circumscris acelui triunghi. Marcaţi centrul acelui cerc. Găsiți centrul de greutate al triunghiului, adică punctul în care triunghiul, dacă ar fi decupat dintr-o bucată de hârtie, s-ar echilibra pe un știft. Centrul de greutate al unui triunghi se află la intersecţia medianelor (linia care uneşte un vârf cu mijlocul laturii opuse). Desenați cele trei înălţimi ale triunghiului (liniile duse din fiecare vârf perpendicular pe latura opusă) și găsiți punctul în care se intersectează.

Toate cele trei puncte pe care tocmai le-ați găsit se află întotdeauna pe o singură linie dreaptă, denumită „linia Euler” a triunghiul”, a explicat Whitney.

Whitney a declarat că această teoremă exemplifică frumusețea și puterea matematicii, care dezvăluie adesea modele surprinzătoare în forme simple și familiare.

Traducere și adaptare după Images: The World’s Most Beautiful Equations